Interpreting Solutions
A feasible solution is a set of values for the decision variables that satisfies all of the constraints in an optimization problem. The set of all feasible solutions defines the feasible region of the problem. Most optimization algorithms operate by first trying to locate any feasible solution, and then attempting to find another (better) feasible solution that improves the value of the objective function. This process of trying to find improving feasible solutions repeats until either no further improvement is possible or some other stopping criteria is met.
As shown in the illustration below, a global optimal solution is one where there is no other feasible solution with a better objective function value. A local optimal solution is one where there is no other feasible solution "in the vicinity" with a better objective function value.
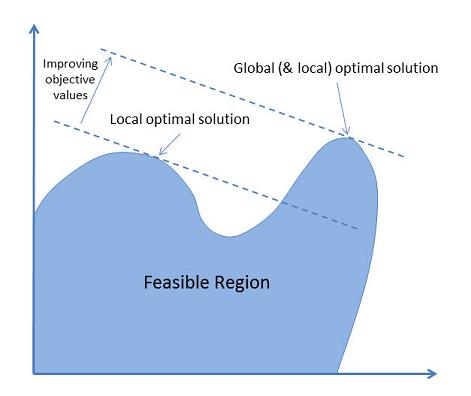
Frontline's Solver products are designed to find global optimum solutions -- but this is not always possible. In many cases, though, you might be happy to find a good solution -- one that is better than the solution you are using now.
Whether the Solver can find a global optimal solution, a local optimal solution, or a good solution depends on the nature of the mathematical relationships between the variables and the objective function and constraints (and the solution algorithm used). For more information, click on the link "What Makes a Model Hard to Solve?"