Artificial neural networks are relatively crude electronic networks of "neurons" based on the neural structure of the brain. They process records one at a time, and "learn" by comparing their classification of the record (which, at the outset, is largely arbitrary) with the known actual classification of the record. The errors from the initial classification of the first record is fed back into the network, and used to modify the networks algorithm the second time around, and so on for many iterations.
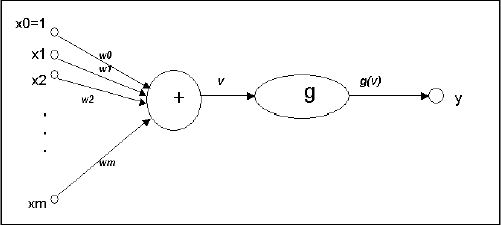
Roughly speaking, a neuron in an artificial neural network is
- A set of input values (xi) and associated weights (wi)
- A function (g) that sums the weights and maps the results to an output (y).
Neurons are organized into layers.
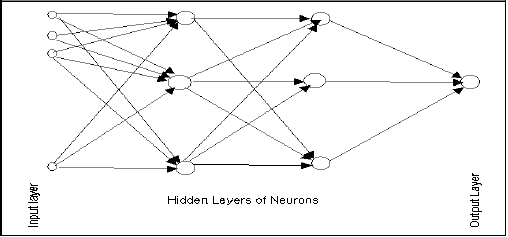
The input layer is composed not of full neurons, but rather consists simply of the values in a data record, that constitute inputs to the next layer of neurons. The next layer is called a hidden layer; there may be several hidden layers. The final layer is the output layer, where there is one node for each class. A single sweep forward through the network results in the assignment of a value to each output node, and the record is assigned to whichever class's node had the highest value.
Training an Artificial Neural Network
In the training phase, the correct class for each record is known (this is termed supervised training), and the output nodes can therefore be assigned "correct" values -- "1" for the node corresponding to the correct class, and "0" for the others. (In practice it has been found better to use values of 0.9 and 0.1, respectively.) It is thus possible to compare the network's calculated values for the output nodes to these "correct" values, and calculate an error term for each node (the "Delta" rule). These error terms are then used to adjust the weights in the hidden layers so that, hopefully, the next time around the output values will be closer to the "correct" values.
The Iterative Learning Process
A key feature of neural networks is an iterative learning process in which data cases (rows) are presented to the network one at a time, and the weights associated with the input values are adjusted each time. After all cases are presented, the process often starts over again. During this learning phase, the network learns by adjusting the weights so as to be able to predict the correct class label of input samples. Neural network learning is also referred to as "connectionist learning," due to connections between the units. Advantages of neural networks include their high tolerance to noisy data, as well as their ability to classify patterns on which they have not been trained. The most popular neural network algorithm is back-propagation algorithm proposed in the 1980's.
Once a network has been structured for a particular application, that network is ready to be trained. To start this process, the initial weights (described in the next section) are chosen randomly. Then the training, or learning, begins.
The network processes the records in the training data one at a time, using the weights and functions in the hidden layers, then compares the resulting outputs against the desired outputs. Errors are then propagated back through the system, causing the system to adjust the weights for application to the next record to be processed. This process occurs over and over as the weights are continually tweaked. During the training of a network the same set of data is processed many times as the connection weights are continually refined.
Note that some networks never learn. This could be because the input data do not contain the specific information from which the desired output is derived. Networks also don't converge if there is not enough data to enable complete learning. Ideally, there should be enough data so that part of the data can be held back as a validation set.
Feedforward, Back-Propagation
The feedforward, back-propagation architecture was developed in the early 1970's by several independent sources (Werbor; Parker; Rumelhart, Hinton and Williams). This independent co-development was the result of a proliferation of articles and talks at various conferences which stimulated the entire industry. Currently, this synergistically developed back-propagation architecture is the most popular, effective, and easy-to-learn model for complex, multi-layered networks. Its greatest strength is in non-linear solutions to ill-defined problems. The typical back-propagation network has an input layer, an output layer, and at least one hidden layer. There is no theoretical limit on the number of hidden layers but typically there are just one or two. Some work has been done which indicates that a maximum of five layers (one input layer, three hidden layers and an output layer) are required to solve problems of any complexity. Each layer is fully connected to the succeeding layer.
As noted above, the training process normally uses some variant of the Delta Rule, which starts with the calculated difference between the actual outputs and the desired outputs. Using this error, connection weights are increased in proportion to the error times a scaling factor for global accuracy. Doing this for an individual node means that the inputs, the output, and the desired output all have to be present at the same processing element. The complex part of this learning mechanism is for the system to determine which input contributed the most to an incorrect output and how does that element get changed to correct the error. An inactive node would not contribute to the error and would have no need to change its weights. To solve this problem, training inputs are applied to the input layer of the network, and desired outputs are compared at the output layer. During the learning process, a forward sweep is made through the network, and the output of each element is computed layer by layer. The difference between the output of the final layer and the desired output is back-propagated to the previous layer(s), usually modified by the derivative of the transfer function, and the connection weights are normally adjusted using the Delta Rule. This process proceeds for the previous layer(s) until the input layer is reached.
Structuring the Network
The number of layers and the number of processing elements per layer are important decisions. These parameters to a feedforward, back-propagation topology are also the most ethereal - they are the "art" of the network designer. There is no quantifiable, best answer to the layout of the network for any particular application. There are only general rules picked up over time and followed by most researchers and engineers applying this architecture to their problems.
Rule One: As the complexity in the relationship between the input data and the desired output increases, the number of the processing elements in the hidden layer should also increase.
Rule Two: If the process being modeled is separable into multiple stages, then additional hidden layer(s) may be required. If the process is not separable into stages, then additional layers may simply enable memorization of the training set, and not a true general solution effective with other data.
Rule Three: The amount of training data available sets an upper bound for the number of processing elements in the hidden layer(s). To calculate this upper bound, use the number of cases in the training data set and divide that number by the sum of the number of nodes in the input and output layers in the network. Then divide that result again by a scaling factor between five and ten. Larger scaling factors are used for relatively less noisy data. If you use too many artificial neurons the training set will be memorized. If that happens, generalization of the data will not occur, making the network useless on new data sets.