Using Models for Risk Analysis
A risk analysis model could be a physical scale model, but it is most often a mathematical model. The model can be created by writing code in a programming language, statements in a simulation modeling language, or formulas in a Microsoft Excel spreadsheet. Regardless of how it is expressed, a risk analysis model will include:
- Model inputs that are uncertain numbers -- we'll call these uncertain variables
- Intermediate calculations as required
- Model outputs that depend on the inputs -- we'll call these uncertain functions
It is essential to realize that model outputs that depend on uncertain inputs are uncertain themselves -- hence we talk about uncertain variables and uncertain functions. To make use of a risk analysis model, we will test many different numeric values for the uncertain input variables, and we'll obtain many different numeric values for the uncertain output functions. We'll use statistics to analyze and summarize all the values for the uncertain functions (and, if we wish, the uncertain variables).
Creating the Model
Since a risk analysis model will be subject to intensive computations, you'll generally want to create the model using available risk analysis tools. An Excel spreadsheet can be a simple, yet powerful tool for creating your model -- especially when paired with Monte Carlo simulation software such as Risk Solver. If your model is written in a programming language, Monte Carlo simulation toolkits like the one in Frontline's Solver SDK Platform provide powerful aids.
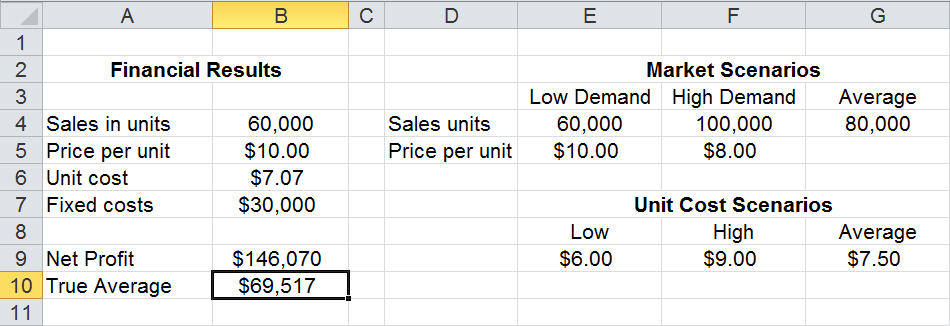
An example model in Excel might look like this, where cell B6 contains a formula =PsiTriangular(E9,G9,F9) to sample values for the uncertain variable Unit cost, and cell B10 contains a formula =PsiMean(B9) to obtain the mean value of Net Profit across all trials of the simulation.
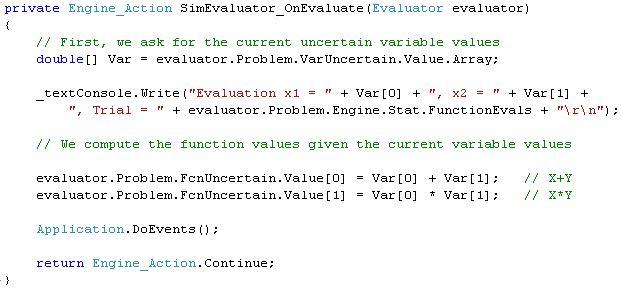
A portion of an example model in the C# programming language might look like this, where the array Var[ ] receives sample values for the two uncertain variables X and Y, and the uncertain function values are computed and assigned to the Problem's FcnUncertain object Value property:
Model Simplification
Like all models, a risk analysis model is a simplification and approximation of reality. The art of modeling involves choices of what essential factors must be included, and what factors may be ignored or safely excluded from the model. As Albert Einstein suggested, a model should be "as simple as possible, but no simpler."
We must also choose what sample values to test for the uncertain variables. Simulation software such as Risk Solver lets us draw sample values from scores of different probability distributions. While we should do our best to choose the right sample values, we derive a great benefit simply by moving from fixed values to almost any reasonable sample of values for an uncertain quantity.
Dr. Sam Savage likes to use the analogy of shaking a ladder before you use it to climb up on a roof. When you do this, you subject the ladder to a random set of forces, to see how it behaves. Even though the forces when you are shaking are not distributed in the same way as the forces when you are climbing, shaking a ladder is still a good “stress test” in advance.
< Back to: The Risk Analysis Process
< Back to: Risk Analysis Tutorial Start Next: Risk Analysis Tools >
