Simulation Models
A simulation model is a mathematical model that calculates the impact of uncertain inputs and decisions we make on outcomes that we care about, such as profit and loss, investment returns, environmental consequences, and the like. Such a model can be created by writing code in a programming language, statements in a simulation modeling language, or formulas in a Microsoft Excel spreadsheet. Regardless of how it is expressed, a simulation model will include:
- Model inputs that are uncertain numbers -- we'll call these uncertain variables
- Intermediate calculations as required
- Model outputs that depend on the inputs -- we'll call these uncertain functions
It's essential to realize that model outputs that depend on uncertain inputs are uncertain themselves -- hence we talk about uncertain variables and uncertain functions. When we perform a simulation with this model, we will test many different numeric values for the uncertain variables, and we'll obtain many different numeric values for the uncertain functions. We'll use statistics to analyze and summarize all the values for the uncertain functions (and, if we wish, the uncertain variables).
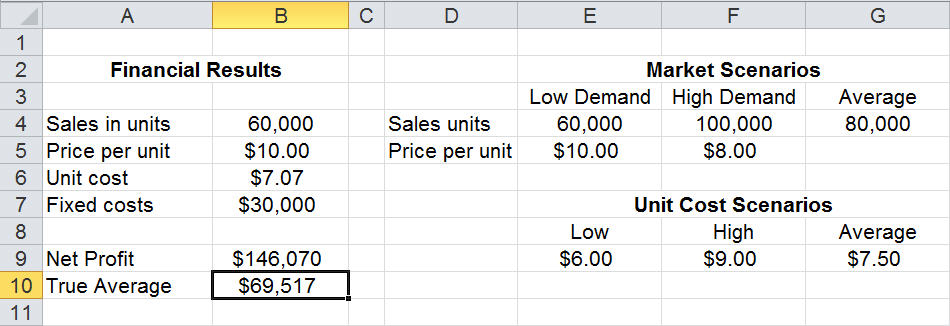
Creating Models in Excel or Custom Programs
An Excel spreadsheet can be a simple, yet powerful tool for creating your model -- especially when paired with Monte Carlo simulation software such as Risk Solver. If your model is written in a programming language, Monte Carlo simulation toolkits like the one in Frontline's Solver Platform SDK provide powerful aids.
An example model in Excel might look like this, where cell B6 contains a formula =PsiTriangular(E9,G9,F9) to sample values for the uncertain variable Unit Cost, and cell B10 contains a formula =PsiMean(B9) to obtain the mean value of Net Profit across all trials of the simulation.
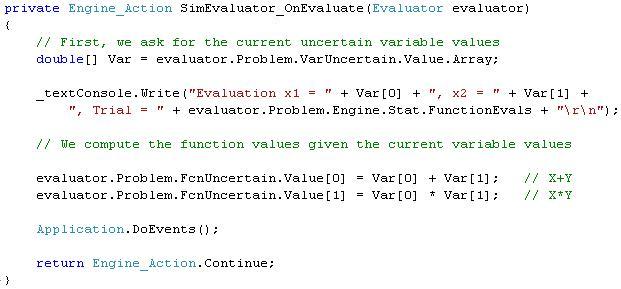
A portion of an example model in the C# programming language might look like this, where the array Var[] receives sample values for the two uncertain variables X and Y, and the uncertain function values are computed and assigned to the Problem's FcnUncertain object Value property:
Choosing Samples for Uncertain Variables
We must also choose what random sample values to use for the uncertain variables. During a simulation, a new sample value will be drawn for every uncertain variable on each trial. Risk Solver provides state-of-the-art random number generators and sampling methods for your simulation needs.
In the simplest case, we might generate random numbers between 0 and 1, and use these as sample values. But in most cases, the range of values, and chance that different values in the range will be drawn on each trial, must be tailored to the uncertain variable. To do this, we normally choose a probability distribution and appropriate parameters for the uncertain variable. As discussed next, selecting appropriate probability distributions is a key step in building a simulation model.
<< Back to: Simulation Tutorial Homepage Next: Probability Distributions >