Gradients, Linearity, and Sparsity
The Product Mix example presented earlier is the simplest type of optimization problem -- a linear programming problem. In this Advanced Tutorial, we'll use the Product Mix example to illustrate several concepts that underlie all optimization problems:
- Derivatives, Gradients, and the Jacobian
- Linearity, Nonlinearity, and Non-Smoothness
- Mixed Linear and Nonlinear Functions and Terms
- Using the LP Coefficient Matrix Directly
- Handling Sparsity in the Jacobian Directly
If you'd like to learn more about simulation as well as optimization, consult our tutorials on simulation, risk analysis and Monte Carlo simulation.
Derivatives, Gradients, and the Jacobian
Recall the formula we wrote for the objective function in the Product Mix example:
Maximize 450 X1 + 1150 X2 + 800 X3 + 400 X4 (Profit)
Consider how this function changes as we change each variable X1, X2, X3 and X4. If we increase X1 by 1, Profit increases by 450; if we decrease X2 by 1, Profit decreases by 1150; and so on. In mathematical terms, 450 is the partial derivative of the objective function with respect to variable X1, and 1150 is its partial derivative with respect to X2.
A function of several variables has an overall "rate of change" called its gradient, which is simply a vector of its partial derivatives with respect to each variable:
( 75, 30, 50 )
Similarly, each constraint has a gradient, which is a vector consisting of the partial derivatives of that function with respect to each decision variable. The first constraint (Glue) has a gradient vector ( 50, 50, 100, 50 ) because it increases by 50 if either X1, X2 or X4 is increased by 1, and it changes by 100 if X3 is changed by 1:
50 X1 + 50 X2 + 100 X3 + 50 X4 <= 5800 (Glue)
5 X1 + 15 X2 + 10 X3 + 5 X4 <= 730 (Pressing)
500 X1 + 400 X2 + 300 X3 + 200 X4 <= 29200 (Pine chips)
500 X1 + 750 X2 + 250 X3 + 500 X4 <= 60500 (Oak chips)
We can combine the gradients of all the constraint functions into a matrix, usually called the Jacobian matrix. The Jacobian for the Product Mix example looks like this:
| 50 | 50 | 100 | 50 |
| 5 | 15 | 10 | 5 |
| 500 | 400 | 300 | 200 |
| 500 | 750 | 250 | 500 |
Almost every "classical" optimization method, for linear and smooth nonlinear problems, makes use of the objective gradient and the Jacobian matrix of the constraints.
Linearity, Nonlinearity, and Non-Smoothness
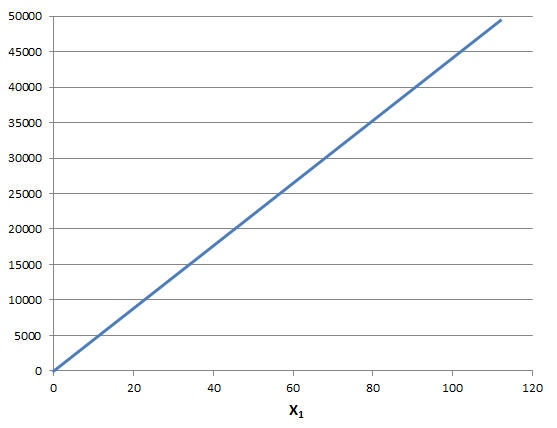
Note that each of these partial derivatives is constant in the Product Mix problem. For example, as shown below, the objective function changes by 450 units, whether X1 moves from 0 to 1 or from 100 to 101. This is true of every linear problem: In a linear programming problem, the objective gradient and Jacobian matrix elements are all constant. In this case, the Jacobian matrix (sometimes with the objective gradient as an extra row) is often called the LP coefficient matrix.
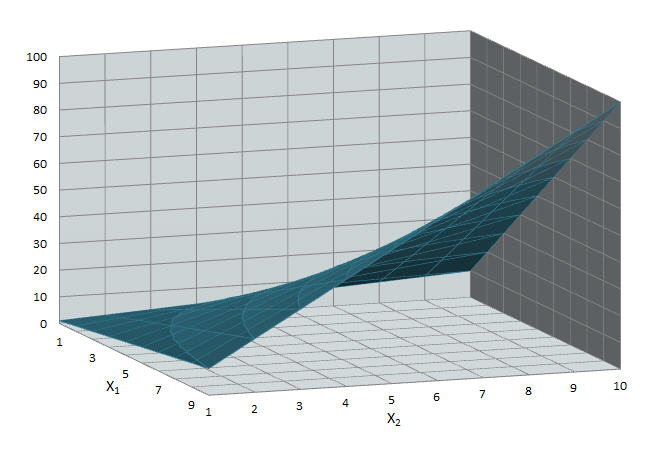
Consider a simple nonlinear function such as X1 * X2 (shown below). If X1 increases by 1 unit, how much will the function change? This change is not constant; it depends on the current value of X2. In a nonlinear optimization problem, the objective gradient and Jacobian matrix elements are not all constant.
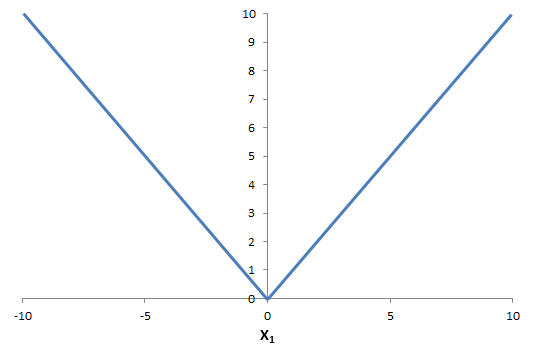
In a smooth nonlinear optimization problem, the partial derivatives may be variable, but they change continuously as the variables change -- they do not "jump" from one value to another. A nonsmooth function, such as ABS(X1) (which returns the absolute value of X1) behaves differently: As shown below, if X1 is positive, it has a partial derivative of 1, but if X1 is negative, it has a partial derivative of -1. The partial derivative is discontinuous at 0, jumping between 1 and -1.
Mixed Linear and Nonlinear Functions and Terms
Many nonlinear (and even nonsmooth) optimization models include some all-linear constraints and / or some variables that occur linearly in all of the constraints. Advanced Solvers for smooth nonlinear and nonsmooth problems can gain speed and accuracy by taking advantage of this fact. The hybrid Evolutionary Solver in the Premium Solver Platform, the Large-Scale GRG Solver engine, and the OptQuest Solver engine are examples of advanced Solvers that work in this way.
Even if a constraint is nonlinear, it may be separated into nonlinear and linear terms. Similarly, some variables may occur only in the linear terms of otherwise nonlinear constraints. Some very advanced Solvers, such as the Large-Scale SQP Solver engine, are designed to exploit these properties of an optimization problem.
(NOTE: Links marked with # intentionally don't work yet.)