The QUADPRODUCT function can be used to define the objective for quadratic programming problems in a single function call, as required for fast problem setup.
The QUADPRODUCT function is designed to supply coefficients for each single variable and each pair of variables, in a manner similar to SUMPRODUCT and DOTPRODUCT.
You supply the arguments of QUADPRODUCT as shown below:
=QUADPRODUCT(variable cells, single coefficients, pair coefficients)
The first argument must consist entirely of decision variable cells. The second and third arguments must consist entirely of cells whose values are constant in the optimization problem; if these cells contain formulas, those formulas must not refer to any of the decision variables. The second argument supplies the coefficients to be multiplied by each single variable in the first argument, using an element-by-element correspondence. The third argument supplies the coefficients to be multiplied by each pair of variables drawn from the first argument. Hence, if there are n cells in the first argument, there must be n2 cells in the third argument. If the variables are represented by x1,x2,...,xn, the single coefficients by a1,a2,...,an, and the pair coefficients by c1,c2,...,cN where N = n2, QUADPRODUCT computes the function:
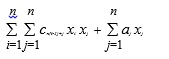
The pairs are enumerated starting with the first cell paired with itself, then the first cell paired with the second cell, and so on. For example, if the first argument consisted of the cells A1:A3, there should be nine cells in the third argument, and the values in those cells will be multiplied by the following pairs in order: A1*A1, A1*A2, A1*A3, A2*A1, A2*A2, A2*A3, A3*A1, A3*A2, and A3*A3. The value returned by QUADPRODUCT is the sum of all of the coefficients multiplied by their corresponding single variables or pairs of variables.
Multiple selections can be used for each argument of QUADPRODUCT, subject to the same considerations outlined above for DOTPRODUCT: You can use the general syntax for multiple selections in Microsoft Excel, but defined names are needed for purposes of fast problem setup, and multiple selections are not accepted by the PSI Interpreter.
