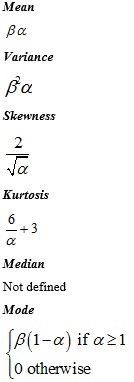PsiGamma (a,β,...)
PsiGamma (α,β) is a flexible distribution with a finite lower bound and decreasing values. PsiExponential, PsiErlang, and PsiChiSquare are special cases of PsiGamma, as explained below. The Gamma distribution is often used to model the time between events that occur with a constant average rate.
When α = 1, the Gamma distribution is the same as an Exponential distribution. If the parameter α is integer, then the Gamma distribution is the same as the Erlang distribution. The Gamma distribution with α = a/2, β = 2 is the same as a Chi Square distribution with parameter a (a degrees of freedom).
If X1, X2, …Xm are independent random variables with Xi ~ PsiGamma (αi,β), then their sum also has a Gamma distribution with parameters (α1 + α2 + …+ αm ,β). Additionally, the Gamma distribution approaches a normal distribution with the same mean and standard deviation as the parameter α approaches infinity.
Alternate Formulation: PsiGammaAlt
PsiGammaAlt is the PsiGamma distribution defined through alternative arguments. Two parameters are required and both must be chosen from the following list: percentile1, percentile2, mean, var, shape or scale. PsiGammaAlt is not supported in Analytic Solver Cloud app.
