PsiCopulaStudent(number_range, position, df, [instance])
Number range: If bivariate, a number between -1 and 1; if multivariate, the Excel cell range where the correlation matrix is located in the Excel spreadsheet, i.e., if the copula is multivariate and the correlation matrix is located in cells N2:P4, then pass N2:P4 for this argument.
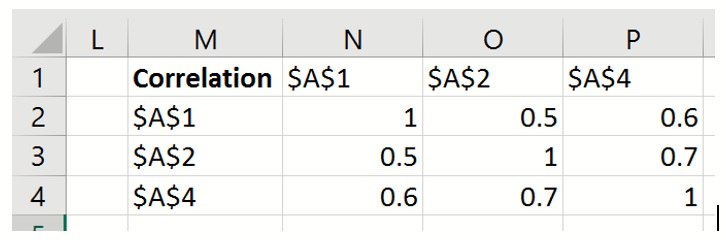
Position: Specifies the uncertain variable index in the correlation matrix. For example, the "2" passed in the formula, =PsiBeta(3, 4, PsiCopulaStudent(N2:P4, 2, 1, "mycop") specifies that the correlation coefficients in the 2nd column of the correlation matrix in cells N2:P4 will be applied to the PsiBeta() uncertain variable.
df: Enter an integer value greater than 1. This parameter specifies the degrees of freedom for the PsiCopulaStudent function. In this example, 1 degree of freedom is used.
Instance: (Optional) Instance is the string name given to the copula. An elliptical copula is explicitly identified by the Instance argument and implicitly identified by the location of the correlation matrix. PsiCopulaStudent() supports multiple copulas using the same correlation matrix. If passing the same type of elliptical copula using the same correlation matrix within the same workbook, this argument must be present. If the workbook contains multiple copulas of different types, then this argument may be omitted. When multiple copulas are present in the same workbook, it is considered "best practice" to use this argument.
Suppose three uncertain variables are present in the same workbook. The three uncertain variables can be correlated using the PsiCopulaStudent property, =PsiCopulaStudent(N2:P4, 1, 1, "mycop"). Since the Instance property is present, the copula is identified explicitly by the name given in the last argument, "mycop". When not passing the Instance property, the PsiCopulaStudent property within each uncertain variable signature, MUST use the same correlation matrix. Otherwise, the correlation between the uncertain variables will not be invoked.
For a complete example of how to use the PsiCopulaStudent() property, see the Modeling Correlation Using Copulas section within the Analytic Solver User Guide.
Theory
If θ = {(v, ∑): v ∈1, ∞, ∈Rmxm where tv is a univariate t distribution with v degrees of freedom, then the Student copula implemented with PsiCopulaStudent() can be written as:
C ( u1, u2, …, um ) = tv, tv-1u1, tv-1 u2, …, tv-1 um
where tv, is the multivariate Student's t distribution with correlation matrix ∑ using v degrees of freedom.
For more information on the theory of Copulas, please see the following references.
Jackel, Peter., “Monte Carlo Methods in Finance”, John Wiley & Sons Ltd, 2002
Nelsen, Roger B., “An Introduction to Copulas”, New York 2006
