Skip to main content
Call Us: 888-831-0333
Free Trial

Fourier Analysis

The Fourier Analysis tool calculates the discrete Fourier transform (DFT) or it's inverse for a vector (column).

This tool computes the discrete Fourier transform (DFT) of the given vector (column) using the Cooley-Tukey decimation-in-time radix-2 algorithm. The vector's length must be a power of 2.

This tool can also compute the inverse discrete Fourier transform (IDFT) of the given complex vector. This vector can have any length. Note: This transform does not perform scaling, so the inverse is not a true inverse.

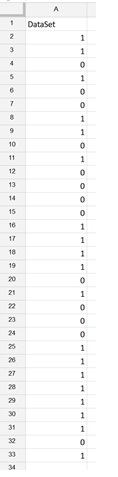
Below is a random series of 0's and 1's simulating a binary signal.

Fourier Analysis Example Dataset

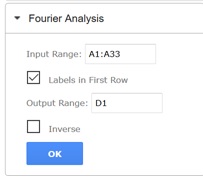
To run the Fourier Analysis:

  1. On the XLMiner Analysis ToolPak pane, click Fourier Analysis
  2. Enter A1:A33 for Input Range. Note: The number of values entered in this argument must be of a size equal to the power of 2, i.e., 2 (2^1), 4 (2^2), 8 (2^3), 16 (2^4), 32 (2^5), 64 (2^6), etc.
  3. Keep "Labels in First Row" selected since Dataset appears in cell A1.
  4. Enter D1 for Output Range.
  5. Click OK.

Note: To compute the inverse discrete Fourier transform of a vector, select Inverse on the pane.

Fourier Analysis Pane

The results are below.

Fourier Analysis Results

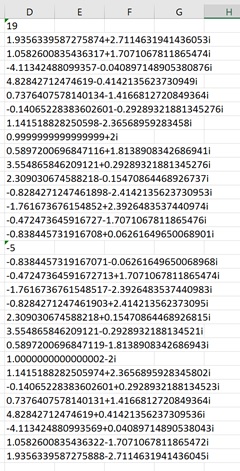
Since the input range included 32 data points, the output also includes 32 points. These points represent a curve that is the amplitude frequency spectrum of the input range.

A complete description of this algorithm and its results is beyond the scope of this guide. For more information, consult standard physics reference texts or articles on the Fourier Transformation.