Generate Synethic Data Options
The following options appear on the Generate Data tabs, Data and Parameters.
Generate Synthetic Data dialog, Data tab
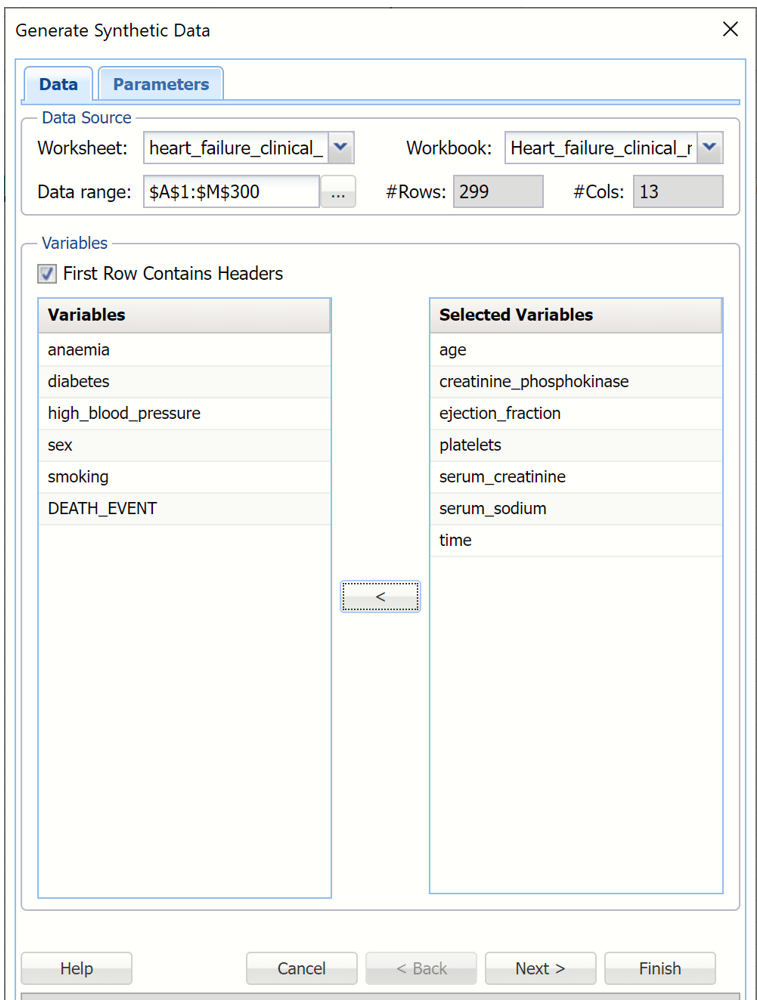
The following options appear on the Data tab of the Generate Synthetic Data dialog. These options pertain to the data source and the variables included.
Variables
All variables in the data source data range are listed in this field. If the first row in the dataset contains headings, select First Row Contains Headers.
Selected Variables
Select a variable(s) in the Variables field, then click > to move the variable(s) to the Selected Variables field. Synthetic data will be generated for the variables appearing in this field.
Generate Synthetic Data dialog, Parameters tab
The following options appear on the Parameters tab of the Generate Synthetic Data dialog. These options pertain to the Distribution Terms, Correlation Fitting and available output.
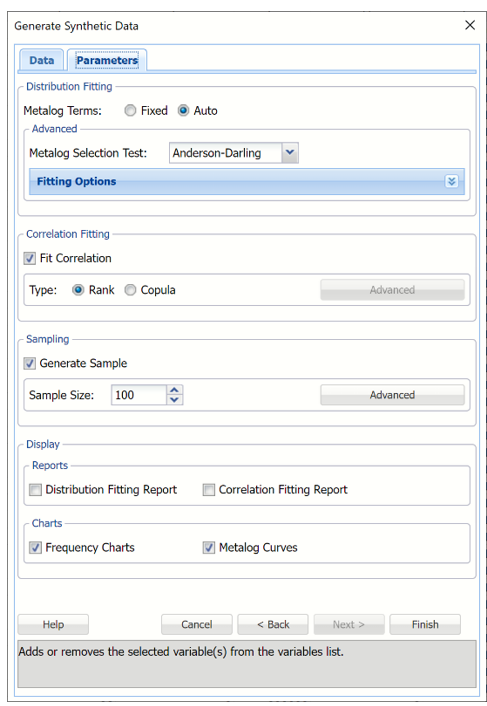
Metalog Terms
- If Fixed is selected, Analytic Solver will attempt to fit and use the Metalog distribution with the specified number of terms entered into the # Terms column. (Only 1 distribution will be fit.) If Fixed is selected, Metalog Selection Test is disabled.
- If Auto is selected, Analytic Solver will attempt to fit all possible Metalog distributions, up to the entered value for Max Terms, and select and utilize the best Metalog distribution according to the goodness-of-fit test selected in the Metalog Selection Test menu.
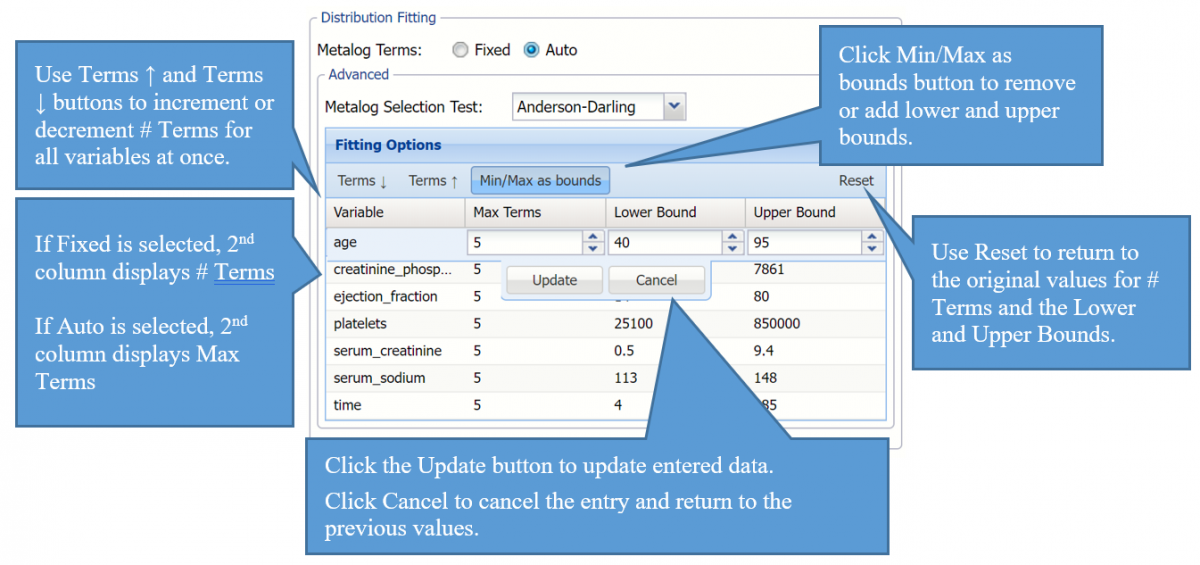
Click the down arrow on the right of Fitting Options to enter either the maximum number of terms (if Auto is selected) or the exact number of terms (if Fixed is selected) for each variable as well as a lower and/or upper bound. By default the lower and upper bounds are set to the variable’s minimum and maximum values, respectively. If no lower or upper bound is entered, Analytic Solver will fit a semi- (with one bound present) or unbounded (with no bounds present) Metalog function.
Distribution Fitting section of the Generate Data dialog
Metalog Selection Test
Click the down arrow to select the desired Goodness-of-Fit test used by Analytic Solver. The Goodness of Fit test is used to select the best Metalog form for each data variable among the candidate distributions containing a different number of terms, from 2 to the value entered for Max Terms. The default Goodness-of-Fit test is Anderson-Darling.
Goodness of Fit Tests:
- Chi Square – Uses the chi-square statistic and distribution to rank the distributions. Sample data is first divided into intervals using either equal probability, then the number of points that fall into each interval are compared with the expected number of points in each interval. The null hypotheses is rejected using a 90% significance level, if the chi-squared test statistic is greater than the critical value statistic. Note: The Chi Square test is used indirectly in continuous fitting as a support in the AIC test. The AIC test must succeed in fitting as this is a necessary condition as well as the fitting of at least one of the tests, Chi Squared, Kolmogorov-Smirnoff, or Anderson-Darling.
- Kolmogorov-Smirnoff –This test computes the difference (D) between the continuous distribution function (CDF) and the empirical cumulative distribution function (ECDF). The null hypothesis is rejected if, at the 90% significance level, D is larger than the critical value statistic.
- Anderson (Default) -Darling –Ranks the fitted distribution using the Anderson Darling statistic, A2 . The null hypothesis is rejected using a 90% significance level, if A2 is larger than the critical value statistic. This test awards more weight to the distribution tails then the Kolmogorov-Smirnoff test.
- AIC – The AIC test is a Chi Squared test corrected for the number of distribution parameters and sample size. AIC = 2 * p – 2 + ln(L) where p is the number of distribution parameters, n is the fitted sample size (number of data points) and ln(L) is the log-likelihood function computed on the fitted data.
- AICc –When the sample size is small, there is a significant chance that the AIC test will select a model with a large number of parameters. In other words, AIC will overfit the data. AICc was developed to reduce the possibility of overfitting by applying a penalty to the number of parameters. Assuming that the model is univariate, is linear in the parameters and has normally-distributed residuals, the formula for AICc is: AICc = AIC + 2 * p *(p + 1) / (n - p − 1) where n = sample size, p = # of parameters. As the sample size approaches infinity, the penalty on the number of parameters converges to 0 resulting in AICc converging to AIC.
- BIC – The Bayesian information criterion (BIC) is defined as: BIC = ln(n) * p - 2 * ln(L) where p is the number of distribution parameters, n is the fitted sample size (number of data points) and ln(L) is the log-likelihood function computed on the fitted data.
- The BICc is the alternative version of BIC, corrected for the sample size BICc = BIC + 2 * p * (p + 1) / (n – p - 1).
- Maximum Likelihood – The (negated) raw value of the estimated maximum log likelihood utilized in tests described above.
Fit Correlation
Select Fit Correlation to fit a correlation between the variables. If this option is left unchecked, correlation fitting will not be performed.
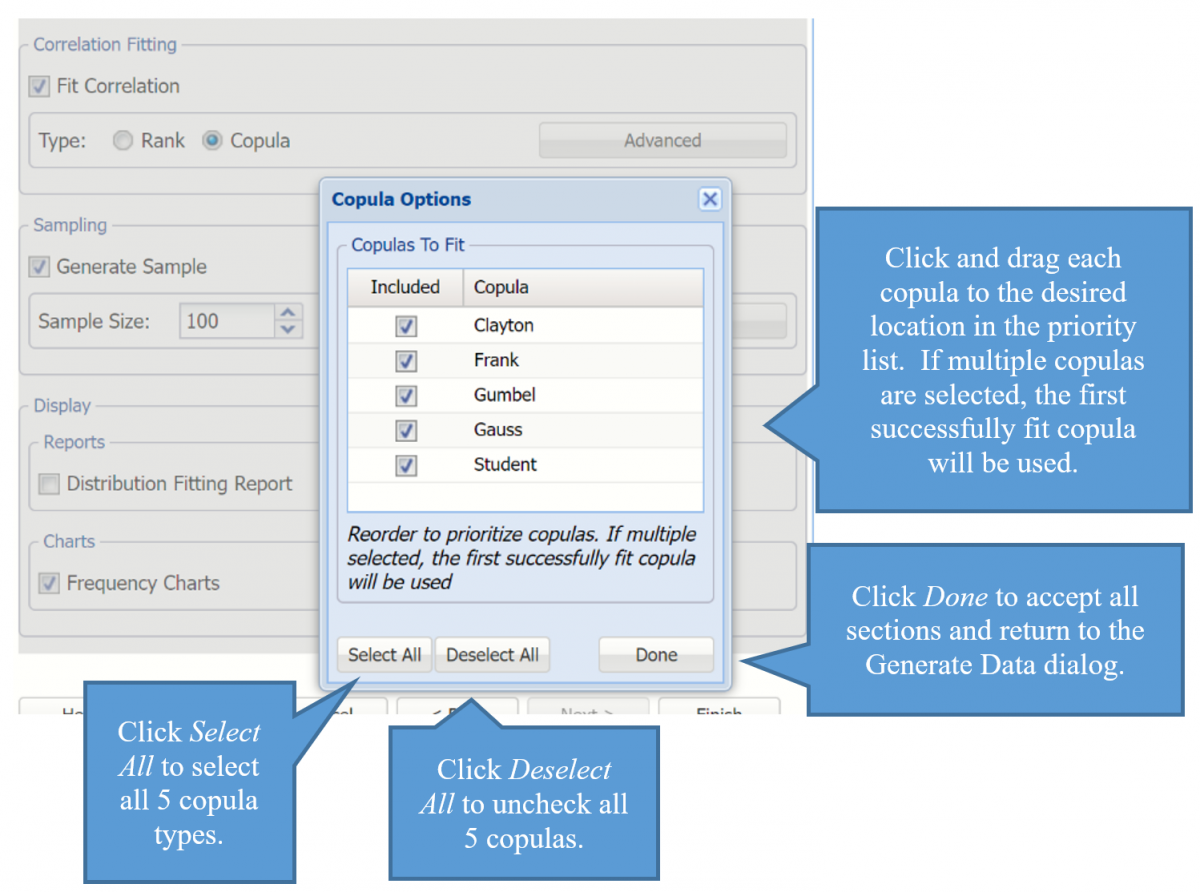
- If Rank is selected Analytic Solver will use the Spearman rank order correlation coefficient to compute a correlation matrix that includes all included variables.
- Selecting Copula opens the Copula Options dialog where you can select and drag five types of copulas into a desired order of priority.
Correlation Fitting section of the Generate Data dialog
Generate Sample
Select Generate Sample to generate synthetic data for each selected variable. Use the Sample Size field to increase the size of the sample generated.
If this option is left unchecked, variable data will be fitted to a Metalog distribution and also correlations, if Fit Correlation is selected, but no synthetic data will be generated.
Click Advanced to open the Sampling Options dialog.
Sampling Options dialog
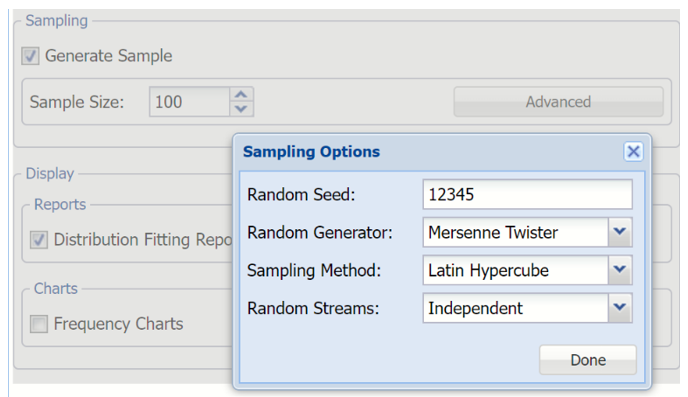
From this dialog, users can set the Random Seed, Random Generator, Sampling Method and Random Streams.
Random Seed
Setting the random number seed to a nonzero value (any number of your choice is OK) ensures that the same sequence of random numbers is used for each simulation. When the seed is zero or the field is left empty, the random number generator is initialized from the system clock, so the sequence of random numbers will be different in each simulation. If you need the results from one simulation to another to be strictly comparable, you should set the seed. To do this, simply type the desired number into the box. (Default Value = 12345)
Random Generator
Use this menu to select a random number generation algorithm. Analytic Solver Data Science includes an advanced set of random number generation capabilities.
Computer-generated numbers are never truly “random,” since they are always computed by an algorithm – they are called pseudorandom numbers. A random number generator is designed to quickly generate sequences of numbers that are as close to statistically independent as possible. Eventually, an algorithm will generate the same number seen sometime earlier in the sequence, and at this point the sequence will begin to repeat. The period of the random number generator is the number of values it can generate before repeating.
A long period is desirable, but there is a tradeoff between the length of the period and the degree of statistical independence achieved within the period. Hence, Analytic Solver Data Science offers a choice of four random number generators:
- Park-Miller “Minimal” Generator with Bayes-Durham shuffle and safeguards. This generator has a period of 231-2. Its properties are good, but the following choices are usually better.
- Combined Multiple Recursive Generator of L’Ecuyer (L’Ecuyer-CMRG). This generator has a period of 2191, and excellent statistical independence of samples within the period.
- Well Equidistributed Long-period Linear (WELL) generator of Panneton, L’Ecuyer and Matsumoto. This generator combines a long period of 21024 with very good statistical independence.
- Mersenne Twister (default setting) generator of Matsumoto and Nishimura. This generator has the longest period of 219937-1, but the samples are not as “equidistributed” as for the WELL and L-Ecuyer-CMRG generators.
- HDR Random Number Generator, designed by Doug Hubbard. Permits data generation running on various computer platforms to generate identical or independent streams of random numbers.
Sampling Method
Use this option group to select Monte Carlo, Latin Hypercube, or Sobol RQMC sampling.
- Monte Carlo: In standard Monte Carlo sampling, numbers generated by the chosen random number generator are used directly to obtain sample values. With this method, the variance or estimation error in computed samples is inversely proportional to the square root of the number of trials (controlled by the Sample Size); hence to cut the error in half, four times as many trials are required.
Analytic Solver Data Science provides two other sampling methods than can significantly improve the ‘coverage’ of the sample space, and thus reduce the variance in computed samples. This means that you can achieve a given level of accuracy (low variance or error) with fewer trials.
- Latin Hypercube (default): Latin Hypercube sampling begins with a stratified sample in each dimension (one for each selected variable), which constrains the random numbers drawn to lie in a set of subintervals from 0 to 1. Then these one-dimensional samples are combined and randomly permuted so that they ‘cover’ a unit hypercube in a stratified manner.
- Sobol RQMC (Randomized QMC). Sobol numbers are an example of so-called “Quasi Monte Carlo” or “low-discrepancy numbers,” which are generated with a goal of coverage of the sample space rather than “randomness” and statistical independence. Analytic Solver Data Science adds a “random shift” to Sobol numbers, which improves their statistical independence.
Random Streams
Use this option group to select a Single Stream for each variable or an Independent Stream (the default) for each variable.
If Single Stream is selected, a single sequence of random numbers is generated. Values are taken consecutively from this sequence to obtain samples for each selected variable. This introduces a subtle dependence between the samples for all distributions in one trial. In many applications, the effect is too small to make a difference – but in some cases, better results are obtained if independent random number sequences (streams) are used for each distribution in the model. Analytic Solver Data Science offers this capability for Monte Carlo sampling and Latin Hypercube sampling; it does not apply to Sobol numbers.
Reports and Charts
Distribution Fitting: Report included on the SyntheticData_Output worksheet includes the number of terms, the coefficients for each term, the lower and upper bounds and the goodnesss of fit statistics used when fitting each Metalog distribution.
Correlation Fitting Report: Displays the correlation matrix on the SyntheticData_Output worksheet
Frequency Charts: Displays the multivariate chart produced by the Analyze Data feature. Double click each chart to view an interactive chart and detailed data (statistics, percentiles and six sigma indices) about each variable included in the analysis. For more information on the Analyze Data feature included in the latest version of Analytic Solver Data Science, see the Exploring Data chapter that appears later in this guide.
Metalog Curves: Select this Chart option to add Metalog distribution curves to each variable displayed in the multivariate chart and interactive charts described above for Frequency Charts.
