PsiCorrelation (cell1,cell2,simulation)
PsiCorrelation returns the Pearson product moment correlation coefficient between the two uncertain variables or functions cell1 and cell2. Correlation is a measure of linear dependence between two uncertain variables or functions. The correlation coefficient can take on values between -1 and +1. A correlation of -1 indicates a perfect negative correlation (the cells move linearly in opposite directions); a correlation of +1 indicates a perfect positive correlation (the cells move linearly in the same direction). If the two random variables are independent, then their correlation coefficient is zero; but if the correlation coefficient is zero, this does not necessarily mean that the two variables are independent. For more information, see “Dependence and Correlation” in the Frontline Solver User Guide chapter “Mastering Simulation and Risk Analysis Concepts.”
Pearson’s product moment correlation coefficient between random variables X and Y is defined as:
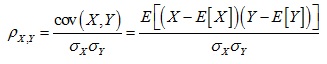
In Monte Carlo simulation, this value is computed from the sample values x[] and y[] over n trials as:
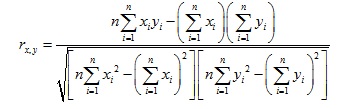
Note: The values returned by PsiCorrelation() are not the same as the correlation coefficients you specify in PsiCorrDepen() and PsiCorrMatrix() property functions. The latter are Spearman rank correlation coefficients and are used to generate sample values from different PSI Distribution functions that are properly correlated. The values returned by PsiCorrelation() are Pearson product moment correlation coefficients, computed from the observed result of the simulation process. You can specify any cell in your model for cell1 and cell2, so you can compute observed correlations between two formula cells, two PSI Distribution cells, or a formula cell and a PSI Distribution cell.
