At this point, you can summarize the problem in the Excel model pictured below, which calculates the Total Revenue based on the number of tickets sold minus the refunds to no shows and compensation to overbooked customers.
- In cell B1, enter the ticket price, $200.
- In cell B2, enter the number of available seats on the airplane, 100.
- In cell B3, enter the formula ROUND(B4,0) to calculate the expected number of no-shows. Assume 10% of tickets sold will result in no-shows. In cell B4, enter 10%.
- In cell B5, enter the percentage refund (50%) to customers who miss the flight.
- Enter the percentage compensation (125%) to customers who are "bumped" from the flight due to overbooking, in cell B6.
- Enter the number of tickets sold (110) in cell B8.
- Use a formula in cell B9 to calculate the number of customers who make the flight, =Number of Tickets Sold – No Shows (=B8 – B3).
- Enter the following formula into cell B10=MAX(0, $B$9 - $B$2), to select the maximum between 0 and the number of people who show up for the flight minus the number of available seats. The MAX function is used to ensure the formula never evaluates to a negative value.
- Enter the formula into cell B12=$B$8 * $B$1 - $B$5 * $B$1 * $B$3 - $B$6 * $B$1 * $B$10, to calculate the total revenue or the revenue after refunds are given to "no-shows" and compensation is paid to overbooked customers.
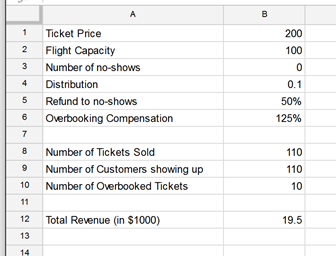
The Total Revenue figure calculated by this model, based on assumed or expected values for the uncertain factors is $19,500.
