Correlation is a statistical measure of the degree to which one variable is related to another. When we observe that two variables are correlated, it may be that one variable is dependent on the other, or that both variables are dependent on a third variable, or that the correlation appeared by chance and there is no real dependence of one variable on the other.
The most common parametric measure of correlation is the Pearson product moment correlation coefficient. You can use the Correlation tool within the XLMiner Analysis Toolpak to compute a correlation matrix that contains the correlation coefficient of each possible pair of variables. The value of the correlation coefficients determine how the two measured variables move together. If they are positively correlated means that if one variable increases, then the 2nd variable will also increase. If they are negatively correlated then when one variable increases, the second variable decreases. The value of a product moment correlation coefficient can range from -1 to +1.
Meaning of Rank Correlation Coefficients
- A correlation coefficient of +1 means that the variables are exactly positively correlated. Coefficients from 0 to +1 will produce varying degrees of positive correlation.
- A correlation coefficient of -1 means that the variables are exactly negatively correlated. Coefficients from 0 to -1 will produce varying degrees of negative correlation.
- A correlation coefficient of 0 means there is no induced relationship between the variables. In practice, one usually uses coefficients less than +1 or -1, and uses 0 only in a correlation matrix that defines relationships among several variables.
Note that a correlation matrix must always have 1’s on the diagonal, because a variable is always perfectly correlated with itself. Also, the matrix must be symmetric: If row 2, column 1 contains 0.8, then row 1, column 2 must also contain 0.8. Finally, the correlation coefficients must be consistent with each other: For example, if uncertain variable 1 is strongly positively correlated with variable 2, and variable 2 is strongly positively correlated with variable 3, then variable 1 cannot be negatively correlated with variable 3.
The example dataset below contains historical closing prices for five stocks.
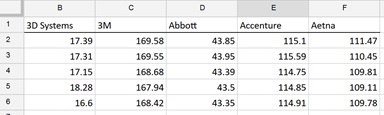
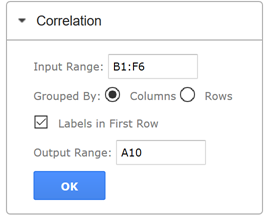
To find the correlation matrix:
- On the XLMiner Analysis ToolPak pane, click Correlation
- Click the Input Range field and enter the cell range B1:F6.
- Keep columns selected for "Grouped By" since our data is arranged by column.
- Leave "Labels in First Row" selected since the first row in the data range includes the column labels.
- Click the Output Range field and then enter cell A10
- Click OK.
The results are shown below.
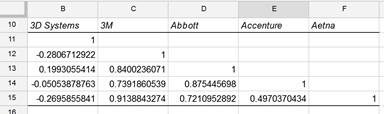
In this example, the closing prices of Aetna and 3M are very strongly correlated, the prices of Aetna and Abbott are strongly correlated and the price of Aetna and Accenture is also rather strongly correlated. However, the closing prices of Aetna and 3D systems are negatively correlated.
