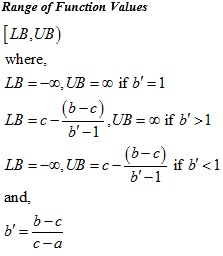PsiMyerson (a,b,c,t,...)
PsiMyerson (a,b,c,t) is a generalized LogNormal/Normal distribution, specified using the bottom percentile (a), 50th percentile (b), top percentile (c) and optional tail percentage parameter (t). This distribution is bounded on the side of the narrower percentile range; when both the bottom and top percentile ranges are equal, then this distribution is unbounded.
If the t parameter (tail percentage) is present then the a and c parameters (bottom and top percentiles) are used to construct a distribution PDF in such a way that the left and right tails (remaining equal) sum up to the desired t parameter value. The top percentile is always symmetric to the bottom percentile. For example, if the bottom percentile equals the 20th percentile, the top percentile will be equal to the 80th percentile.
The default option for parameter t is 0.50 which means that the left tail and the right tail each equal 0.25. As a result, parameter a (bottom percentile) is the 25th percentile and parameter c (top percentile) is the 75th percentile.
This distribution, developed by Dr. Roger Myerson, is used to model random variables when the only information available is the percentile values, and optionally, a tail percentage parameter indicating the probability of values being within the specified percentiles. If the specified percentiles are equidistant (measured by the parameter b’ below), then the Myerson distribution is equivalent to a Normal distribution. When the 50th percentile is equal to the geometric mean of the top and bottom percentiles, then the Myerson distribution is equivalent to the LogNormal distribution.