PsiMeanCI (cell,confidence level,simulation)
PsiMeanCI returns the confidence “half-interval” for the estimated mean value (returned by the PsiMean() function) for the specified uncertain function cell, at the specified confidence level (for example 0.95 or 0.99). If μ is the value returned by PsiMean() and δ is the value returned by PsiMeanCI(), the true mean is estimated to lie within the interval μ - δ to μ + δ.
The confidence level can be interpreted as follows: If we compute a large number of independent estimates of confidence intervals on the true mean of the uncertain function, each based on n observations with n sufficiently large, then the proportion of these confidence intervals that contain the true mean of the function should equal the confidence level.
If σ2 (n) is the sample variance from n trial values, a = 1 – confidence level, and tn-1, 1-α/2 is the upper 1-α/2 critical point of the Student’s t-distribution with n-1 degrees of freedom, the confidence half-interval δ is computed as:
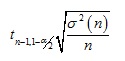
The confidence interval measures the precision with which we have estimated the true mean. Larger half widths imply that there is a lot of variability in our estimates. The above formula for the half-width assumes that the individual xis are normally distributed; when this is not the case, the above formula still gives us an approximate confidence interval on the true mean of the uncertain function.
Two additional arguments are utilized when a Psi Statistic function is used with Dimensional Modeling: Struc_format and Param_slice.
PsiMeanCI (cell,confidence level,simulation,struc_format,param_slice)
Struc_format: This argument is an optional argument entered as a string. If omitted, all cube values will be printed in a single column. If “dims” is passed for this argument, the Psi Statistic function will print all dimensions in the cube with their lengths so the user can be advised of the size of the cubes and will be able to estimate the range needed when entering the Psi Statistic function as an array formula. If “vals” is passed for this argument, the result values will be displayed along with the dimension elements in the form of a relational or pivot table. Please see the Simulation example in the Dimensional Modeling chapter in Frontline Solvers User Guide for more information on this function. It’s also possible to use this argument to return the name of a specific element in a cube containing one or more structural dimensions.
To use this argument to return the value of a specific element in a 1-dimensional cube (containing a structural dimension), use the form: “ [StructuralDimisension1].[Element1]”. To use this argument to return the value of a 2-dimensional cube (containing structural dimensions), use the form: “[StructuralDimension1].[Element],[StructuralDimension2].[Element]”.
To use this argument to return the value of a N-dimensional cube (containing structural dimensions), use the form: “[StructuralDimension1].[Element],[StructuralDimension2].[Element],…,[StructuralDimensionN].[Element]”.
Param_slice: The param_slice argument is an optional string argument specifying the desired element “slice” for the parametric dimensions. If omitted the elements selected in the pane will be used. It’s also possible to use this argument to return the value of a specific element in a cube containing one or more parametric dimensions.
To use this argument to return the value of a specific element in a 1-dimensional cube (containing a parametric dimension), use the form: “[ParametricDimisension1].[Element1]”.
To use this argument to return the value of a 2-dimensional cube (containing parametric dimensions), use the form: “[ParametricDimension1].[Element],[ParametricDimension2].[Element]”.
